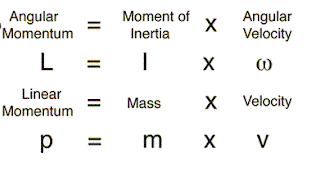28-Nov, 2016 . Lab #21: Physical Pendulum Lab

Lab #21: Physical Pendulum Lab
                                                                                                                Dahlia - Carlos - Luis - Bimaya

28-Nov-2016

The purpose of the lab#19 is to derive an expression for the period of various physical pendulums. Then, verify the theoretical value by experiment.
In this lab, our group found periods of 3 objects: A ring, a semicircle, and a triangle.
First, we calculate the moment of inertia about the pivot and the period of the object as a physical pendulum. After that, we measured the actual period of it by connecting with Logger Pro. 
And finally, we compared the experimental value vs. the theoretical result.
Part A.
 Pendulum: a ring of finite thickness and a little notch cut out at the top.
1. Physical measurements of the ring:
In order to calculate the period of the ring as a physical pendulum, we needed to measure the ring's radii ( R-outer and R-inner)
This was what we had:

Actually, in the picture, we also had the dimensions of the semicircle and the triangle as well. So, in part B and part C for the semicircle and the triangle, I do not need to show the dimensions again.

2. Derive expression for the ring:
Then, we calculated the period of the ring as a physical pendulum.

With the dimensions we had, we plugged to the formula we just derived, and the period was 0.7155 s.

3. Measure actual period:
First, we assumed that the little notch cut out at the top was the pivot of the moment.

Then, to be able to record, we attached a thin stick note to the bottom of the ring. When oscillation took place, the photo gate could detect from the stick note.

After that, we opened a file named "Pendulum Timer.cmbl" to set up photo-gate to record the period of the metal ring. Finally, we gently tap the ring so the oscillation occurs at a small angle displacement and collected data.

and the period we had was:

4. Compare the experimental result and the theoretical result.
The theoretical value: 0.7155 s
The experimental value: 0.7089 s
The percent error = (0.7155-0.7089)*100%/0.7089=0.93%

Part B.
 Pendulum: An isosceles triangle of height H and base B, and a semicircular disk of radius R
Because the triangle and the semicircle did not have a hole to be a pivot, so we used some paper clips to make pivot for objects.
1. Physical measurements:
 The dimensions of the semicircle and the triangle were shown before in part A

2. An Isosceles triangle, base B, height H, and oscillating about its apex:
a. Derive expression:
We calculated the period of the triangle as a physical pendulum.

Plugged the height and the base, we had the period T = 0.764 s.

b. Measure actual period:
First, we knew that the pivot was its apex.
Then, to be able to record, we attached a thin stick note to the midpoint of its base. When oscillation took place, the photo gate could detect from the stick note.
After that, we gently tap the triangle so the oscillation occurs at a small angle displacement and collected data.

and the period we had was:

d. Compare the experimental result and the theoretical result.

The theoretical value: 0.764 s
The experimental value: 0.755 s
The percent error = (0.764-0.755)*100%/0.764=1.18%

3. An Isosceles triangle, base B, height H, and oscillating about the midpoint of its base:

a. Derive expression:

We calculated the period of the triangle as a physical pendulum.

Plugged the height and the base, we had the period T = 0.6828 s.

b. Measure actual period:

First, we knew that the pivot was the midpoint of its base.

Then, to be able to record, we attached a thin stick note to the apex. When oscillation took place, the photo gate could detect from the stick note.

After that, we gently tap the triangle so the oscillation occurs at a small angle displacement and collected data.

and the period we had was:

d. Compare the experimental result and the theoretical result.

The theoretical value: 0.6828 s

The experimental value: 0.6755s

The percent error = (0.6828-0.6755)*100%/0.6828=1.07%

4. A semicircular plate of radius R, oscillating about the midpoint of its base

a. Derive expression:

We calculated the period of the semicircle as a physical pendulum.

Plugged the height and the base, we had the period T = 0.838 s.

b. Measure actual period:

First, we knew that the pivot was the midpoint of its base.

Then, to be able to record, we attached a thin stick note to the point on its edge, directly above the midpoint of the base. When oscillation took place, the photo gate could detect from the stick note.

After that, we gently tap the semicircle so the oscillation occurs at a small angle displacement and collected data.

and the period we had was:

d. Compare the experimental result and the theoretical result.

The theoretical value: 0.838 s

The experimental value: 0.824 s

The percent error = (0.838-0.824)*100%/0.838=1.67%

5. A semicircular plate of radius R, oscillating about the point on its edge, directly above the midpoint of the base

a. Derive expression:

We calculated the period of the semicircle as a physical pendulum.

Plugged the height and the base, we had the period T = 0.821 s.

b. Measure actual period:

First, we knew that the pivot was the point on its edge, directly above the midpoint of the base

Then, to be able to record, we attached a thin stick note to the midpoint of the base. When oscillation took place, the photo gate could detect from the stick note.

After that, we gently tap the semicircle so the oscillation occurs at a small angle displacement and collected data.

and the period we had was:

d. Compare the experimental result and the theoretical result.

The theoretical value: 0.821 s

The experimental value: 0.807 s

The percent error = (0.821-0.807)*100%/0.821=1.71%

Part C: Conclusion

Now, I listed the comparison, the percent error of each object

- The ring: 0.93%

- The triangle oscillating about its apex: 1.18%

- The triangle oscillating about the midpoint of its base: 1.07%

- The semicircle oscillating about the midpoint of its base: 1.67%
- The semicircle oscillating about a top point on its edge:  1.71%
The error occurred because of some reasons such as the uncertainties in the measurements of the dimensions of the objects; Some frictions due to the air as well as the pivot; The paper clip made the distance a little bit higher than calculation in the theoretical result.
The extra mass of the pivot clip, located where they were should not measurably affect the period because of at the final formula, the mass was cancelled already.

21-Nov, 2016 . Lab #20: Conservation of linear and Angular Momentum

Lab #20: Conservation of linear and Angular Momentum
                                                                                                                 Dahlia - Carlos - Luis - Bimyia

21-Nov-2016

The purpose of the lab#19 is to confirm that the linear momentum and angular momentum are conservative.
In order to set up this lab, we need the Model ME-9821 Rotational Accessory Kit and the ME-9279A Rotational Dynamics Apparatus. We as students were not able to actually perform the lab ourselves so Professor Wolf is the one that demonstrated it to the whole class. 

I. Theory

because L = I.w
                 = m.r^2.v/r
                 = m.v.r
                 = p.r
Thus, to show the conservation of linear and angular momentum, we had to do 3 things. First, we had to calculate the angular momentum based on the moment of inertia and angular velocity. Then, we had to figure out the angular momentum based on linear momentum. And finally, we compared the both results.

II. Angular momentum based on linear momentum
there was a ball slid down a ramp some height off the ground. Then it hit the ground at some point L away from the end of the ramp. And we had a piece of carbon copy paper was placed on the floor to find exactly where the ball hit. 

This was the actual value we had when measured distances.

Then, we figured out the velocity as well as measured the mass of the ball in order to calculate the linear momentum.

Because the angular momentum = mass of ball * velocity*radius from the axis. 

So, we could not calculate the angular momentum yet, but this was found later.

III. Angular momentum based on inertia and angular velocity
This part of the lab required the use of a rotational apparatus. The same ball would be launched from the ramp shown and caught by a little ball catcher attached to the top of a torque pulley on top of one of the rotating disks. 

Once the ball hit the ball catcher, the disk would begin to rotate. 

First, we had to find the moment of inertia. To find the moment of inertia, we needed to know the angular acceleration of the rotated object. Then, we used the formula from lab 16 to calculate the inertia momentum

the slope of the graph was the angular acceleration.
then, we had

Then, we let the ball run and found the angular velocity

Finally, we could calculate the angular momentum based on inertia and angular velocity. when doing this experience, we also know the radius from the axis. Therefore, we could calculate the angular momentum based on the linear momentum as well.

VI. Calculation and comparison
This was what we had

Now we could calculate the angular momentum
because we did 2 trials, so we had 2 angular momentums.

Then, we figured out the percent difference.

	Linear M.	inertia	% diff.
Trial #1	0.00311	0.00246	23.3393178
Trial #2	0.00156	0.00174	-10.9090909

V. Conclusion
We already know that the linear momentum is conservative. now, according to this lab, we can assume that the angular momentum is also conservative. even though the percent difference of 2 ways to calculate the angular momentum are pretty high. this occurred because of some reasons such as the uncertainty of the radius from the axis, losing energy when the ball rotated as well as moved at the ramp, and the uncertainty when we measured the distances at the beginning. 

21-Nov, 2016 . Lab #19: Conservation of Energy/Conservation of Angular Momentum

Lab #19: Conservation of Energy/Conservation of Angular Momentum
                                                                                                                                          Dahlia - Carlos

21-Nov-2016

The purpose of the lab#19 is to confirm that the conservation of energy and conservation of angular momentum is true. In this lab, we release a meter stick, pivoted at or near one end, from a horizontal position. Right when the meter stick reaches the bottom of its swing it collides in-elastically with a blob of clay. The meter stick and clay continue to rotate to some final position. Like the picture:

Then, we calculated the height that the meter stick raised by using the conservation of energy and conservation of angular momentum as well as measured it from the experience. Finally, we compared them and concluded that the conservation of energy and conservation of angular momentum was still true or not.

I. Theory:

This was what we had, there was a meter stick rotated around pivot apart from 1 end 10 cm. 

Because the stick did not rotate around center of mass, so we had to calculate the inertia momentum around the pivot.

Then, we used the the conservation of energy to find the angular velocity of the stick before the collapse.

After that, we used the conservation of angular momentum to find the value of angular velocity after the collapse.

Finally, once again, we used the conservation of energy to figure out the height that the stick raised.

So, the theoretical data were: 
- Height of clay: 0.1356 m
- Height of center of mass of stick: 0.5603 m
II. Experience
After we had the theoretical data, we set up the meter stick and let it go.

 Then, we captured it and put it into log pro to measure the height that the stick raised.

So, the experimental data were: 
- Height of clay: 0.1411 m
- Height of center of mass of stick: 0.5898 m

III. Find percent error
I entered theoretical data as well as experimental data to a sheet of excel to find the percent error

	theory	exp.	%error
clay	0.1356	0.1411	4.05605
cm	0.560288	0.5989	6.89146

IV. Conclusion

Conservation of energy and conservation of angular momentum allowed us to calculate the angular velocity before the stick and clay collided.  We also used moments of inertia, the parallel axis theorem, and sum of individual components of GPE to calculate our theoretical value.  In the end, we had a 4.1% error with the raising of clay and 6.9% of the raising of the center of mass of stick. The error occurred because of some reason such as: Losing energy when the meter stick and clay stick together; Losing energy because of Air resistance; and the uncertainty of the original position when release the meter stick.

14-Nov, 2016 . Lab #18: Moment of Inertia and Frictional Torque

Lab #18: Moment of Inertia and Frictional Torque
                                                                                                                                          Dahlia - Rafael

14-Nov-2016

The purpose of the lab#18 is to determine the time an object takes when it is connected with a rotated disk by a string in a given distance. And then, compared the time it takes by experimental value and theoretical value.
I. Theory:
To calculate the time, we had to have to know the acceleration of the object. To find it, we tried to figure out the angular acceleration of the disk.

So we had:

So, the angular acceleration of the disk depended on the radius of a small pulley, the mass of the cart, the angle of track, the inertia of the disk and the angular acceleration of friction.
And finally, we could calculate the time it takes 

II. Produce:
1. Inertia of the disk:
I=(1/2)*(mass of disk)*(radius of disk)^2
but the issue here was we did not know what the mass of the disk was; thus, we tried to figure out the mass of disk.
So, first, we measured dimensions of the disk-pulley.

Then, we calculated the mass of the disk.

And we came up with the mass of the disk was 4.18 kg.
Now, we could easy to calculate the inertia of the disk when it rotated around it center with mass = 4.18 kg and radius =0.1005 m
the inertia = 0.02092 kg*m^2
2. Angular acceleration of friction:
We recorded the rotated disk and put it in lab pro to figure out the angular acceleration of friction.
First, we marked a tape on the disk, then recorded every points of this tape.
Then, we pointed them in the log pro, and we get the graph of position vs. time

The log pro also provided the velocity of this tape vs. time.
So, we could have the angular velocity of this tape was velocity/radius
and the angular acceleration of friction was the slope of the graph angular velocity vs. time.
and it was 1.58 rad/s^2
Once again, I listed needed data to calculate the angular acceleration of disk.

Then, I found the time it took to travel 1 m with the angle 40 degrees.

The theoretical time was 11.276 s. 
3. Experimental value:
we set up the cart connected with the rotated disk by a string. This cart traveled in the track made 40 degrees with the horizontal. Then, we used timer to get the time this cart travel 1 m.

This was what we had after 3 trials:

4. Comparing the theoretical value with the experimental value:
I entered these data to a sheet of excel and calculate the percent error.

III. Conclusion:
 When Comparing  to the theoretical time vs the experimental time, the percent error came out only -0.67% error, and this was a really good result. 

Errors occur because of the friction between the carts wheels and the track. and the string not completely parallel with the inclined track. 

From now on, if we do not have a timer, and we need to find the time the cart takes in a  certain of distance, we can use the angular acceleration of the disk to know the needed time.