21-Nov, 2016 . Lab #19: Conservation of Energy/Conservation of Angular Momentum

Lab #19: Conservation of Energy/Conservation of Angular Momentum
                                                                                                                                          Dahlia - Carlos

21-Nov-2016

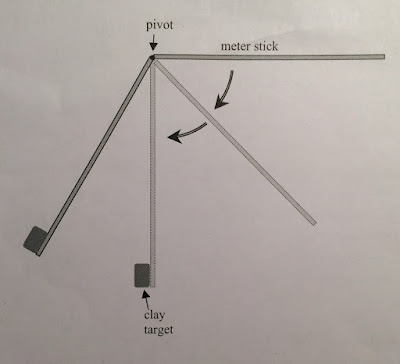
The purpose of the lab#19 is to confirm that the conservation of energy and conservation of angular momentum is true. In this lab, we release a meter stick, pivoted at or near one end, from a horizontal position. Right when the meter stick reaches the bottom of its swing it collides in-elastically with a blob of clay. The meter stick and clay continue to rotate to some final position. Like the picture:

Then, we calculated the height that the meter stick raised by using the conservation of energy and conservation of angular momentum as well as measured it from the experience. Finally, we compared them and concluded that the conservation of energy and conservation of angular momentum was still true or not.

I. Theory:

This was what we had, there was a meter stick rotated around pivot apart from 1 end 10 cm. 

Because the stick did not rotate around center of mass, so we had to calculate the inertia momentum around the pivot.

Then, we used the the conservation of energy to find the angular velocity of the stick before the collapse.

After that, we used the conservation of angular momentum to find the value of angular velocity after the collapse.

Finally, once again, we used the conservation of energy to figure out the height that the stick raised.

So, the theoretical data were: 
- Height of clay: 0.1356 m
- Height of center of mass of stick: 0.5603 m
II. Experience
After we had the theoretical data, we set up the meter stick and let it go.

 Then, we captured it and put it into log pro to measure the height that the stick raised.

So, the experimental data were: 
- Height of clay: 0.1411 m
- Height of center of mass of stick: 0.5898 m

III. Find percent error
I entered theoretical data as well as experimental data to a sheet of excel to find the percent error

	theory	exp.	%error
clay	0.1356	0.1411	4.05605
cm	0.560288	0.5989	6.89146

IV. Conclusion

Conservation of energy and conservation of angular momentum allowed us to calculate the angular velocity before the stick and clay collided.  We also used moments of inertia, the parallel axis theorem, and sum of individual components of GPE to calculate our theoretical value.  In the end, we had a 4.1% error with the raising of clay and 6.9% of the raising of the center of mass of stick. The error occurred because of some reason such as: Losing energy when the meter stick and clay stick together; Losing energy because of Air resistance; and the uncertainty of the original position when release the meter stick.