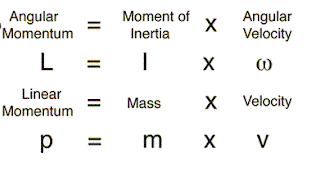Lab #20: Conservation of linear and Angular Momentum
Dahlia - Carlos - Luis - Bimyia
Dahlia - Carlos - Luis - Bimyia
21-Nov-2016
The purpose of the lab#19 is to confirm that the linear momentum and angular momentum are conservative.
In order to set up this lab, we need the Model ME-9821 Rotational Accessory Kit and the ME-9279A Rotational Dynamics Apparatus. We as students were not able to actually perform the lab ourselves so Professor Wolf is the one that demonstrated it to the whole class.
I. Theory
because L = I.w
= m.r^2.v/r
= m.v.r
= p.r
Thus, to show the conservation of linear and angular momentum, we had to do 3 things. First, we had to calculate the angular momentum based on the moment of inertia and angular velocity. Then, we had to figure out the angular momentum based on linear momentum. And finally, we compared the both results.
II. Angular momentum based on linear momentum
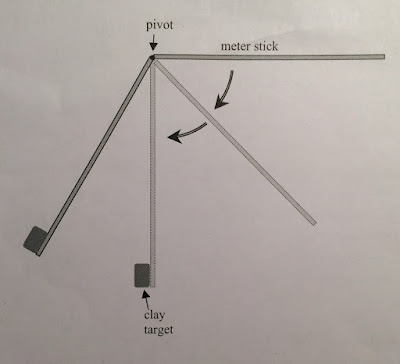
there was a ball slid down a ramp some height off the ground. Then it hit the ground at some point L away from the end of the ramp. And we had a piece of carbon copy paper was placed on the floor to find exactly where the ball hit.
This was the actual value we had when measured distances.
Then, we figured out the velocity as well as measured the mass of the ball in order to calculate the linear momentum.
This part of the lab required the use of a rotational apparatus. The same ball would be launched from the ramp shown and caught by a little ball catcher attached to the top of a torque pulley on top of one of the rotating disks.
Once the ball hit the ball catcher, the disk would begin to rotate.
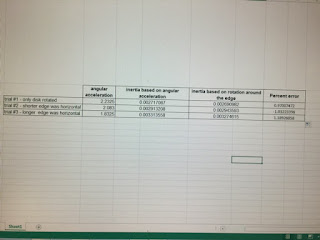
First, we had to find the moment of inertia. To find the moment of inertia, we needed to know the angular acceleration of the rotated object. Then, we used the formula from lab 16 to calculate the inertia momentum
the slope of the graph was the angular acceleration.
then, we had
Then, we let the ball run and found the angular velocity
Finally, we could calculate the angular momentum based on inertia and angular velocity. when doing this experience, we also know the radius from the axis. Therefore, we could calculate the angular momentum based on the linear momentum as well.
VI. Calculation and comparison
This was what we had
Now we could calculate the angular momentum
because we did 2 trials, so we had 2 angular momentums.
Then, we figured out the percent difference.
V. Conclusion
We already know that the linear momentum is conservative. now, according to this lab, we can assume that the angular momentum is also conservative. even though the percent difference of 2 ways to calculate the angular momentum are pretty high. this occurred because of some reasons such as the uncertainty of the radius from the axis, losing energy when the ball rotated as well as moved at the ramp, and the uncertainty when we measured the distances at the beginning.
In order to set up this lab, we need the Model ME-9821 Rotational Accessory Kit and the ME-9279A Rotational Dynamics Apparatus. We as students were not able to actually perform the lab ourselves so Professor Wolf is the one that demonstrated it to the whole class.
I. Theory
because L = I.w
= m.r^2.v/r
= m.v.r
= p.r
Thus, to show the conservation of linear and angular momentum, we had to do 3 things. First, we had to calculate the angular momentum based on the moment of inertia and angular velocity. Then, we had to figure out the angular momentum based on linear momentum. And finally, we compared the both results.
II. Angular momentum based on linear momentum
there was a ball slid down a ramp some height off the ground. Then it hit the ground at some point L away from the end of the ramp. And we had a piece of carbon copy paper was placed on the floor to find exactly where the ball hit.
This was the actual value we had when measured distances.
Then, we figured out the velocity as well as measured the mass of the ball in order to calculate the linear momentum.
So, we could not calculate the angular momentum yet, but this was found later.
III. Angular momentum based on inertia and angular velocityThis part of the lab required the use of a rotational apparatus. The same ball would be launched from the ramp shown and caught by a little ball catcher attached to the top of a torque pulley on top of one of the rotating disks.
Once the ball hit the ball catcher, the disk would begin to rotate.
First, we had to find the moment of inertia. To find the moment of inertia, we needed to know the angular acceleration of the rotated object. Then, we used the formula from lab 16 to calculate the inertia momentum
the slope of the graph was the angular acceleration.
then, we had
Then, we let the ball run and found the angular velocity
Finally, we could calculate the angular momentum based on inertia and angular velocity. when doing this experience, we also know the radius from the axis. Therefore, we could calculate the angular momentum based on the linear momentum as well.
VI. Calculation and comparison
This was what we had
Now we could calculate the angular momentum
because we did 2 trials, so we had 2 angular momentums.
Then, we figured out the percent difference.
| Linear M. | inertia | % diff. | |
| Trial #1 | 0.00311 | 0.00246 | 23.3393178 |
| Trial #2 | 0.00156 | 0.00174 | -10.9090909 |
We already know that the linear momentum is conservative. now, according to this lab, we can assume that the angular momentum is also conservative. even though the percent difference of 2 ways to calculate the angular momentum are pretty high. this occurred because of some reasons such as the uncertainty of the radius from the axis, losing energy when the ball rotated as well as moved at the ramp, and the uncertainty when we measured the distances at the beginning.