14-Nov, 2016 . Lab #17: Moment of Inertia of a Uniform Triangle

Lab #17: Moment of Inertia of a Uniform Triangle
                                                                                                                                          Dahlia - Rafael

14-Nov-2016

The purpose of the lab#17 is to determine the moment of inertia of a right triangular thin plate around its center of mass, for two perpendicular orientations of the triangle.
I. Theory:
The parallel axis theorem states that:

Because the limits of integration are simpler if we calculate the moment of inertia around a vertical end of the triangle, thus we can easy to calculate the inertia round center of mass based on the inertia about the vertical end.
The picture below shows how to calculate the inertia of uniform triangle around one end vertical as well as around it's center of mass.
First, I found center of mass of triangle. 

Then, I found the inertia when the triangle rotated around the edge and around the center of mass.

Thus, based on theory, the inertia of a triangle around center of mass is (1/18)*(mass of triangle)*(length of the horizontal edge)^2.
Moreover, there is another way to calculate the moment inertia based on Newton's second law and free body diagram.

Thus, the inertia of triangle around center of mass based on the mass of hanging mass, the radius of a rotation disk and the angular acceleration.


II. Procedure:
The pictures below are showing how we set up the kit when doing this experiment. Because this inertial is based on the angular acceleration, we did the same progress with lab #16 to get value of angular acceleration. we did three trials:
1 with the disks

1 with triangle horizontal larger side, 

and 1 with a triangle with horizontal smaller side.

This is what we had from the lab pro by sensor. The slope of the angular velocity vs. time was the angular acceleration.

So, after 3 trials, I had:

and this is the data of hanging mass as well as the radius of disk.

(from the lab #16.)

Therefore, hanging mass was 0.025 kg, and radius of the rotated disk was  0.0249 m.

Then, I measured dimensions of the triangle.

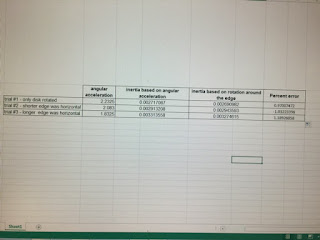
Then, I entered these value to a sheet of excel and from formulas, I calculated value of theoretical inertia based on rotation around the edge and value of experimental inertia based on angular acceleration.

and I calculated the percent error of them.

III. Conclusion:

By finding the difference between the moment of inertia of a rotating system and then the moment of inertia of a triangular plate mounted about its center in two positions, we were able to find the moments of inertia of the triangular plate itself.  Then, we calculated the moment of inertia about the triangular plate's edge using calculus, and plugged all of this into the equation for the parallel axis theorem to compare our mathematical results for moment of inertia about the triangle's center to our experimental results for moment of inertia about the triangle's center. 

The result came out was pretty good. The percent error was only within 2% at all 3 trials.
 Our errors in theoretical and experimental values could have been made from a number of factors: the mass of the triangular plate may not have been completely in uniform density; the air being released to spin the rotating disks may have fluctuated, causing acceleration to fluctuate; there also could have been error in the measurements.